Enthüllung der Mathematik hinter Kryptowährungen: Eine Reise von Halbaddierern zu Hash-Funktionen
In der faszinierenden Welt der Kryptowährungen spielt die Mathematik eine entscheidende, wenn auch oft übersehene Rolle. Dieser Artikel nimmt Sie mit auf eine Reise durch die mathematischen und kryptographischen Prinzipien, die Kryptowährungen antreiben. Von den einfachsten Konzepten wie Halbaddierern bis hin zu komplexen Themen wie Hash-Funktionen und elliptischer Kurven-Kryptographie werden wir die Geheimnisse hinter der Technologie entschlüsseln, die die moderne Finanzwelt revolutioniert.
Die Bausteine: Halbaddierer
In der Welt der Kryptowährungen spielen mathematische Konzepte eine entscheidende Rolle. Einer der grundlegendsten Bausteine in dieser Hinsicht ist der Halbaddierer. In diesem Abschnitt werden wir uns eingehend mit dem Konzept des Halbaddierers befassen und seine Bedeutung im Kontext von Kryptowährungen erörtern.
Was ist ein Halbaddierer?
Ein Halbaddierer ist eine einfache Schaltung, die in der digitalen Elektronik verwendet wird, um die Addition von zwei einzelnen Bits durchzuführen. Er hat zwei Eingänge und zwei Ausgänge: einen für die Summe und einen für den Übertrag (Carry).
Halbaddierer-Schaltkreis
Der Halbaddierer-Schaltkreis besteht in der Regel aus einem UND-Gatter und einem XOR-Gatter. Das XOR-Gatter wird verwendet, um die Summe der beiden Eingangsbits zu berechnen, während das UND-Gatter den Übertrag erzeugt.
Halbaddierer-Diagramm und -Gatter
Das Diagramm eines Halbaddierers zeigt die Verbindung zwischen den Eingangsbits, den Gattern und den Ausgangsbits. Die Gatter sind so angeordnet, dass sie die gewünschten Ausgänge erzeugen.
Abbildung 1: Schematische Darstellung eines Halbaddierers
Hier würde eine schematische Darstellung des Halbaddierers gezeigt, die die Verbindung der Gatter und die Flussrichtung der Bits illustriert.
Bedeutung im Kontext von Kryptowährungen
Halbaddierer sind die Grundbausteine für komplexere Rechenoperationen, die in der Kryptographie und somit auch in Kryptowährungen eine Rolle spielen. Sie sind Teil der Algorithmen, die für die Erzeugung von Hash-Funktionen und für kryptographische Verfahren verwendet werden.
Von Halbaddierern zu Volladdierern
Einleitung
Nachdem wir die Grundlagen und die Bedeutung von Halbaddierern im Kontext von Kryptowährungen verstanden haben, ist es an der Zeit, einen Schritt weiter zu gehen. In diesem Abschnitt werden wir die Konzepte von Volladdierern untersuchen und ihre Rolle in der digitalen Welt erläutern.
Die Grenzen von Halbaddierern
Halbaddierer sind zwar nützlich für einfache Additionen, stoßen jedoch schnell an ihre Grenzen, wenn es um komplexere Rechenoperationen geht. Sie können nur zwei Bits addieren und haben keinen Eingang für einen Übertrag aus einer vorherigen Addition, was sie für mehrstellige Additionen ungeeignet macht.
Wie Volladdierer diese Grenzen überwinden
Ein Volladdierer ist eine Erweiterung des Halbaddierers und kann drei Bits addieren: zwei Eingangsbits und ein Übertragsbit aus einer vorherigen Addition. Dies ermöglicht die Addition von mehrstelligen Binärzahlen.
Der Übergang von Halbaddierern zu Volladdierern in Computersystemen
In Computersystemen und speziell in der Kryptographie werden oft Volladdierer verwendet, um komplexe Rechenoperationen durchzuführen. Sie sind integraler Bestandteil von Algorithmen, die für Verschlüsselung und Datenintegrität in Kryptowährungen sorgen.
Volladdierer spielen eine entscheidende Rolle in der Kryptographie, die die Grundlage für die Sicherheit und Integrität von Kryptowährungen bildet. Sie ermöglichen komplexere Rechenoperationen, die für die Erzeugung von Hash-Funktionen und kryptographischen Schlüsseln erforderlich sind.
Zahlentheorie und Kryptographie
Nachdem wir die Grundlagen der Addierer verstanden haben, ist es an der Zeit, uns mit der Zahlentheorie zu befassen. Dieses mathematische Fachgebiet ist von zentraler Bedeutung für die Kryptographie, die wiederum das Herzstück von Kryptowährungen bildet.

Einführung in die Zahlentheorie
Die Zahlentheorie ist ein Bereich der Mathematik, der sich mit den Eigenschaften und Beziehungen von Zahlen, insbesondere ganzen Zahlen, beschäftigt. Sie befasst sich mit Konzepten wie Primzahlen, Teilbarkeit und Kongruenz, die in der Kryptographie eine wichtige Rolle spielen.
Primzahlen und ihre Bedeutung
Primzahlen sind Zahlen, die nur durch sich selbst und die Zahl 1 teilbar sind. Sie sind von zentraler Bedeutung für Verschlüsselungsalgorithmen, da sie bestimmte mathematische Eigenschaften besitzen, die die Sicherheit erhöhen.
Wie Zahlentheorie in der Kryptographie verwendet wird
In der Kryptographie werden zahlentheoretische Konzepte verwendet, um sichere Verschlüsselungsalgorithmen zu entwickeln. Beispielsweise basieren viele Public-Key-Algorithmen auf dem Problem der Zerlegung großer Zahlen in ihre Primfaktoren, ein Problem, das mit heutigen Computern nicht effizient gelöst werden kann.
Die Zahlentheorie bietet die mathematische Grundlage für die Verschlüsselungstechniken, die in Kryptowährungen verwendet werden. Ohne die Zahlentheorie wäre es nicht möglich, sichere Transaktionen und die Integrität der Blockchain zu gewährleisten.
Anwendungsbeispiele in Kryptowährungen
- RSA-Algorithmus: Ein Public-Key-Verschlüsselungsverfahren, das auf der Zahlentheorie basiert.
- Elliptische Kurven: Ein weiteres zahlentheoretisches Konzept, das in modernen Kryptowährungen verwendet wird.
Hash-Funktionen: Das Rückgrat der Blockchain
Nachdem wir die Bedeutung der Zahlentheorie für die Kryptographie erörtert haben, wenden wir uns nun einem weiteren entscheidenden Element zu: den Hash-Funktionen. Diese Funktionen sind das Rückgrat der Blockchain-Technologie, die die Grundlage für Kryptowährungen bildet.
Was sind Hash-Funktionen?
Eine Hash-Funktion ist ein Algorithmus, der eine Eingabe (oder “Nachricht”) nimmt und eine Ausgabe von fester Länge erzeugt. Die Ausgabe, oft als Hash-Wert bezeichnet, sollte für jede einzigartige Eingabe einzigartig sein.
Wie funktionieren Hash-Funktionen?
Hash-Funktionen nehmen eine Eingabe und führen eine Reihe von Berechnungen durch, um einen einzigartigen Hash-Wert zu erzeugen. Diese Funktionen sind so konzipiert, dass sie schnell sind, aber es extrem schwierig ist, den ursprünglichen Eingabewert aus dem Hash-Wert abzuleiten.
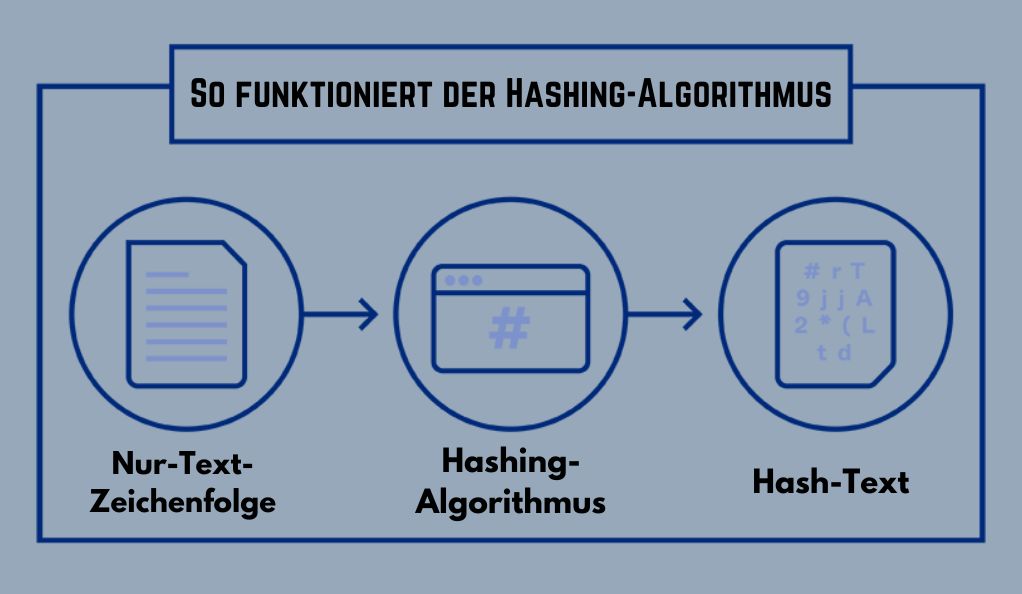
Bedeutung von Hash-Funktionen in der Blockchain
In der Blockchain-Technologie werden Hash-Funktionen verwendet, um die Integrität der Daten zu gewährleisten. Jeder Block in der Blockchain enthält einen Hash des vorherigen Blocks, was eine unveränderliche Kette von Blöcken schafft.
Anwendungsbeispiele in Kryptowährungen
- Transaktionsüberprüfung: Hash-Funktionen werden verwendet, um die Echtheit von Transaktionen zu überprüfen.
- Erstellung von digitalen Signaturen: Hash-Funktionen sind entscheidend für die Erstellung sicherer digitaler Signaturen in Kryptowährungstransaktionen.
Hash-Funktionen und Sicherheit
Die Sicherheit einer Hash-Funktion ist entscheidend für die Integrität der gesamten Blockchain. Eine schwache Hash-Funktion könnte die Tür für Angriffe wie das Double-Spending öffnen.
Elliptische Kurven-Kryptographie: Die Avantgarde
Nachdem wir die Grundlagen von Hash-Funktionen und deren Bedeutung für die Blockchain verstanden haben, ist es an der Zeit, uns mit einer der fortschrittlichsten Technologien in der Kryptographie zu befassen: der elliptischen Kurven-Kryptographie (ECC).
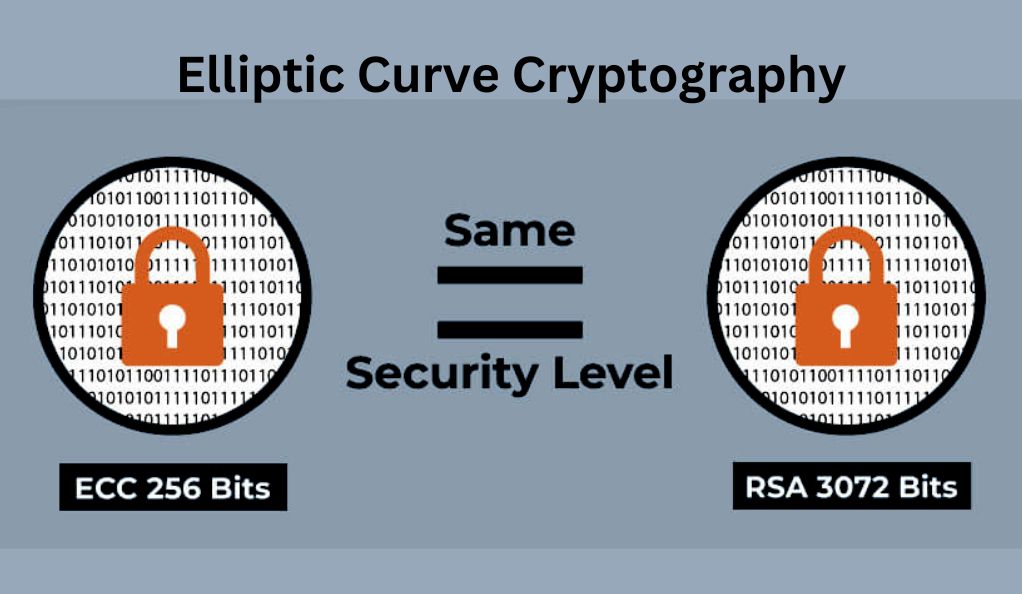
Was ist elliptische Kurven-Kryptographie?
Elliptische Kurven-Kryptographie ist eine Form der Public-Key-Kryptographie, die auf der Algebra und Geometrie von elliptischen Kurven über endlichen Körpern basiert. Sie bietet ein höheres Sicherheitsniveau bei geringerem Rechenaufwand im Vergleich zu traditionellen Methoden wie RSA.
Grundlagen der elliptischen Kurven
Eine elliptische Kurve ist ein geometrisches Objekt, das durch eine Gleichung der Form �2=�3+��+�y2=x3+ax+b definiert ist. In der Kryptographie werden spezielle Typen von elliptischen Kurven verwendet, die bestimmte Sicherheitseigenschaften aufweisen.
ECC in der Praxis: Anwendungsbeispiele
- Bitcoin und ECC: Bitcoin verwendet ECC für die Erstellung von digitalen Signaturen, die die Echtheit von Transaktionen bestätigen.
- Sichere Kommunikation: ECC wird in sicheren Kommunikationssystemen wie SSL/TLS verwendet.
Vorteile von ECC
- Höhere Sicherheit: ECC bietet bei gleicher Schlüssellänge eine höhere Sicherheit als andere Public-Key-Verfahren.
- Effizienz: ECC erfordert weniger Rechenleistung und Speicherplatz, was sie ideal für mobile Geräte und IoT-Anwendungen macht.
Herausforderungen und Bedenken
Trotz der Vorteile gibt es auch Herausforderungen, wie die Auswahl sicherer Kurven und die Anfälligkeit für bestimmte Arten von Angriffen.
Mining und Proof of Work
Nachdem wir uns mit den fortgeschrittenen Technologien wie elliptischen Kurven befasst haben, ist es nun an der Zeit, einen Blick auf das Herzstück vieler Kryptowährungen zu werfen: das Mining und das Konzept des Proof of Work (PoW).
Was ist Mining?
Mining ist der Prozess, durch den neue Blöcke zur Blockchain hinzugefügt werden. Miner verwenden spezialisierte Hardware, um komplexe mathematische Probleme zu lösen, die zur Validierung und Sicherung von Transaktionen erforderlich sind.
Das Konzept des Proof of Work
Proof of Work ist ein Konsensalgorithmus, der in vielen Kryptowährungen verwendet wird. Er erfordert, dass Miner eine rechenintensive Aufgabe lösen, um das Recht zu erhalten, einen neuen Block zur Blockchain hinzuzufügen.
Mathematische Herausforderungen im Mining
Im Rahmen des PoW müssen Miner komplexe mathematische Rätsel lösen. Diese Rätsel sind oft hash-basiert und erfordern einen erheblichen Rechenaufwand, um gelöst zu werden.
Tabelle 3: Vergleich zwischen PoW und PoS (Proof of Stake)
| Kriterium | Proof of Work | Proof of Stake |
|---|---|---|
| Energieverbrauch | Hoch | Niedrig |
| Sicherheit | Sehr sicher | Sicher |
| Dezentralität | Hoch | Mittel |
| Skalierbarkeit | Niedrig | Hoch |
Mining und PoW sind entscheidend für die Sicherheit und Stabilität von Kryptowährungen. Sie sorgen für die Integrität der Blockchain und schützen das Netzwerk vor Angriffen wie Double Spending.
Zukünftige Trends: PoW vs. PoS
Es gibt eine wachsende Debatte über die Nachhaltigkeit von PoW wegen seines hohen Energieverbrauchs. Alternativen wie Proof of Stake (PoS) werden als umweltfreundlichere Optionen erforscht.
Zukünftige Trends: Quantencomputing und Kryptowährungen
Nachdem wir die verschiedenen Aspekte der Mathematik und Kryptographie in Kryptowährungen untersucht haben, ist es an der Zeit, einen Blick in die Zukunft zu werfen. Ein besonders interessantes Thema ist die mögliche Auswirkung des Quantencomputings auf Kryptowährungen.
Was ist Quantencomputing?
Quantencomputing ist eine aufstrebende Technologie, die Quantenmechanik nutzt, um Berechnungen durchzuführen. Im Gegensatz zu klassischen Computern, die Bits verwenden, arbeiten Quantencomputer mit Quantenbits oder Qubits, die eine Superposition von Zuständen ermöglichen.
Potenzielle Auswirkungen auf Kryptographie
Quantencomputer haben das Potenzial, viele der heute verwendeten kryptographischen Algorithmen zu brechen. Beispielsweise könnte ein leistungsfähiger Quantencomputer die RSA-Verschlüsselung in einer praktikablen Zeit knacken.
Tabelle 4: Klassische vs. Quanten-Kryptographie
| Kriterium | Klassische Kryptographie | Quanten-Kryptographie |
|---|---|---|
| Sicherheitsniveau | Hoch | Sehr hoch |
| Rechenanforderungen | Moderat | Hoch |
| Anwendungsbereiche | Breit | Noch begrenzt |
Anpassung der Kryptowährungen an Quantentechnologie
Es gibt bereits Forschungen und Entwicklungen, um kryptographische Algorithmen zu schaffen, die gegen Angriffe durch Quantencomputer resistent sind. Diese werden als “quantensichere” Algorithmen bezeichnet.
Schlussfolgerung
In diesem Artikel haben wir eine umfassende Reise durch die Welt der Kryptowährungen unternommen, beginnend bei den grundlegenden mathematischen Bausteinen wie Halb- und Volladdierern bis hin zu fortschrittlichen Technologien wie elliptischen Kurven und Quantencomputing. Die Mathematik und Kryptographie sind das unsichtbare Rückgrat, das die Sicherheit, Integrität und Funktionsfähigkeit von Kryptowährungen gewährleistet. Mit dem Aufkommen neuer Technologien wie dem Quantencomputing wird es immer wichtiger, die mathematischen Grundlagen und kryptographischen Algorithmen ständig weiterzuentwickeln, um die Zukunft der Kryptowährungen zu sichern.
